Parallelizing the Berkowitz Algorithm with Python
Overview
During academic research I had the opportunity to get familiar with and implement the Samuelson–Berkowitz algorithm for computing the characteristic polynomial of a square matrix whose entries may be elements of any unital commutative ring. The algorithm is division-free, thus may be applied to a wider range of algebraic structures. In addition to many mathematical properties, the Berkowitz algorithm is highly parallelizable allowing utilization of modern hardware for computing characteristic polynomials for large matrices. This ability to distribute computation across multiple cores or processors can lead to significant performance improvements, making it a compelling choice for high-performance computing tasks.
With the release of Python 3.14 and official support of free threading, it was tempting to test performance of the Berkowitz algorithm implementation across different Python versions and parallelization primitives. Writing a correct benchmark is notoriously hard. The Internet is full of conflicting benchmarks, each with its own set of conclusions. Benchmarking parallel algorithms is even trickier because now “parallel is executed everything”.

Fig.1. Multithreading: Theory vs Practice
Results can often be misleading or inconclusive, leading to false conclusions about practical speedup. So, of course, I decided to add another "flawed" benchmark to the long list of such benchmarks.
Implementation
The Berkowitz algorithm is implemented in pure Python 3.13+ without any third-party dependencies, focusing on simplicity and correctness. The implementation is inspired by the approach used in SymPy, a well-known symbolic mathematics library. All results are verified against SymPy's implementation to ensure accuracy.
The algorithm is CPU-bound, meaning it does not involve any I/O operations. Parallelization is achieved by distributing the computation of Toeplitz-like matrices across multiple workers. This enables computationally expensive tasks, such as matrix multiplication, to be processed concurrently, improving performance for larger matrices.
The concurrent.futures package from Python’s standard library provides a simple, high-level interface for concurrency, abstracting away much of the complexity involved in concurrent programming. This makes the development process smoother and reduces the risk of common mistakes typically associated with concurrency. Thanks to the well-designed API, it was possible to implement parallel versions of the algorithm using threads, processes and sub-interpreters with minimal changes to the core code.
The core idea behind parallelization in the implementation is to distribute tasks like computing Toeplitz-like matrices across multiple workers. The concurrent.futures package allows seamless switching between different types of workers. The parallel version of the algorithm uses the following worker classes:
1 2 3 4 5 | WORKER_CLASSES: Final[dict] = { 'interpreter': futures.InterpreterPoolExecutor, # requires Python>=3.14 'process': futures.ProcessPoolExecutor, 'thread': futures.ThreadPoolExecutor, } |
The above dictionary defines three worker types: interpreters, processes and threads, allowing for easy substitution based on the available resources. Here’s an example of how the code uses the worker class to submit tasks for parallel execution:
1 2 3 4 5 6 7 | with WORKER_CLASSES[worker_class](max_workers=workers) as executor: for future in futures.as_completed( executor.submit(__toeplitz_matrix, A, n) for n in range(N, 1, -1) ): T = future.result() transforms[len(T) - 3] = T |
This code demonstrates how easy it is to switch between different execution engines. Whether using threads, processes or sub-interpreters, the implementation logic remains the same, and the parallelization is handled transparently by concurrent.futures. This flexibility ensures that the algorithm can take full advantage of available hardware without changing the underlying code structure.
Benchmark
Writing a benchmark was almost as hard as implementing the algorithm. The goal was to evaluate the performance of the parallel Berkowitz algorithm by comparing execution times across four configurations: serial execution, parallel execution using threads, processes and interpreters (where available).
Key Features of the benchmark code:
Matrix Size Variability: The benchmark tests matrices of sizes ranging from small 2x2 matrices to larger 200x200 matrices.
Parallel Worker Types: It compares the serial version of the algorithm with parallel versions that use threads, processes, and sub-interpreters (if available).
Progress Feedback: A progress bar shows the status of the benchmark as it runs, providing a clear indication of how far along the test is.
Statistical Averaging: The execution times are averaged over a set number of samples (default 10) to account for any variability in performance.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 | import platform from argparse import ArgumentParser from itertools import zip_longest from math import floor from os import path from random import randint from statistics import mean from sys import version_info from time import perf_counter from typing import Any, Callable, Generator, Iterable from berkowitz import berkowitz SUB_INTERPRETERS_AVAILABLE: bool = version_info.minor > 13 def progress( iterable: Iterable, total: int, bars: int = 50, message: str = '' ) -> Generator: for idx, value in enumerate(iterable, start=1): yield idx, value print( 'Progress{}: │{:░<50}│ {:.2f}%/100% ({}/{})'.format( message, '█' * floor(idx * bars / total), idx * 100 / total, idx, total ), end='\r' ) print() def time_func( func: Callable, samples: int, *args: Any, **kwargs: Any ) -> float: timing: list = [] for _ in range(samples): start = perf_counter() func(*args, **kwargs) timing.append(perf_counter() - start) return mean(timing) def main() -> None: cmd_parser = ArgumentParser( description="Benchmark suite for Berkowitz's algorithm" ) cmd_parser.add_argument( '-w', '--workers', type=int, default=4, help='number of parallel workers' ) cmd_parser.add_argument( '-s', '--samples', type=int, default=10, help='number of measurement samples (must be >=1)' ) cmd_parser.add_argument( '-o', '--output', default='.', help='path to output directory' ) cmd_args = cmd_parser.parse_args() if cmd_args.workers < 1: cmd_parser.error('Number of workers must be greater or equal to 1') if cmd_args.samples < 1: cmd_parser.error('Number of samples must be greater or equal to 1') if not path.isdir(cmd_args.output): cmd_parser.error(f'"{cmd_args.output}" directory doesn\'t exist') filename_prefix = ( f'{platform.system()}_{platform.machine()}' f'_python_{version_info.major}' f'_{version_info.minor}_{version_info.micro}' f'_workers_{cmd_args.workers}' ).lower() serial_times: list = [] parallel_interpreter_times: list = [] parallel_thread_times: list = [] parallel_process_times: list = [] y = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 30, 50, 70, 100, 130, 150, 170, 200] for _, n in progress(y, len(y)): matrix = [[randint(-10000, 10000) for j in range(n)] for i in range(n)] serial_times.append(time_func(berkowitz, cmd_args.samples, matrix)) if cmd_args.workers > 1: parallel_thread_times.append( time_func( berkowitz, cmd_args.samples, matrix, cmd_args.workers, ) ) parallel_process_times.append( time_func( berkowitz, cmd_args.samples, matrix, cmd_args.workers, 'process', ) ) if SUB_INTERPRETERS_AVAILABLE: parallel_interpreter_times.append( time_func( berkowitz, cmd_args.samples, matrix, cmd_args.workers, 'interpreter', ) ) with open(path.join(cmd_args.output, f'{filename_prefix}.csv'), 'w') as fd: fd.write('Matrix size (n×n),Serial,Interpreters,Threads,Processes\n') for row in zip_longest( y, serial_times, parallel_interpreter_times, parallel_thread_times, parallel_process_times, fillvalue='' ): fd.write(','.join(map(str, row)) + '\n') if __name__ == '__main__': main() |
Benchmark results are stored in a .csv file, recording matrix size and execution times for serial, thread-based, process-based, and interpreter-based executions. This allows to analyze the effectiveness of parallelization and observe any performance improvements across different configurations.
python3 benchmark.py --help
usage: benchmark.py [-h] [-w WORKERS] [-s SAMPLES] [-o OUTPUT]
Benchmark suite for Berkowitz's algorithm
options:
-h, --help show this help message and exit
-w, --workers WORKERS
number of parallel workers
-s, --samples SAMPLES
number of measurement samples (must be >=1)
-o, --output OUTPUT path to output directory
The benchmark was executed on a Fedora 41 Linux system with an Intel(R) Core(TM) i5-10400 CPU @ 2.90GHz inside Docker containers based on the python:3.13-alpine and python:3.14-alpine images. The free threaded Python 3.14 version was compiled manually within a container running the alpine:3 image.
Example command for running the benchmark in the Docker container:
docker run --security-opt seccomp=unconfined \
--privileged \
--rm \
-it \
-w "/var/opt" \
-v "$(pwd):/var/opt" \
"python:3.14-alpine" \
python3 benchmark.py --workers 4
The following charts visualize the benchmark results across Python 3.13 and 3.14, using different measurement configurations.
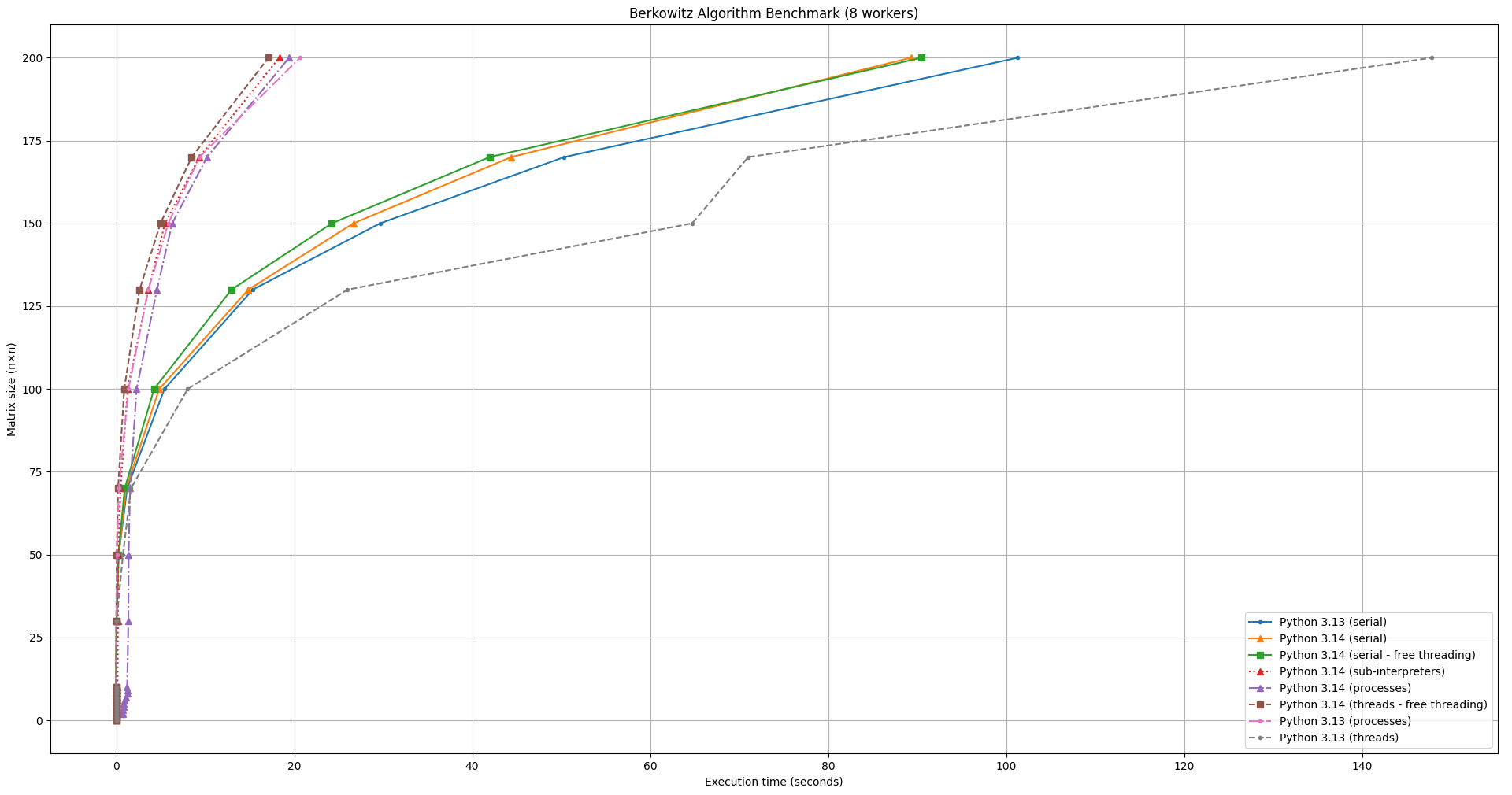
Fig.2. Benchmark Result: Line Chart
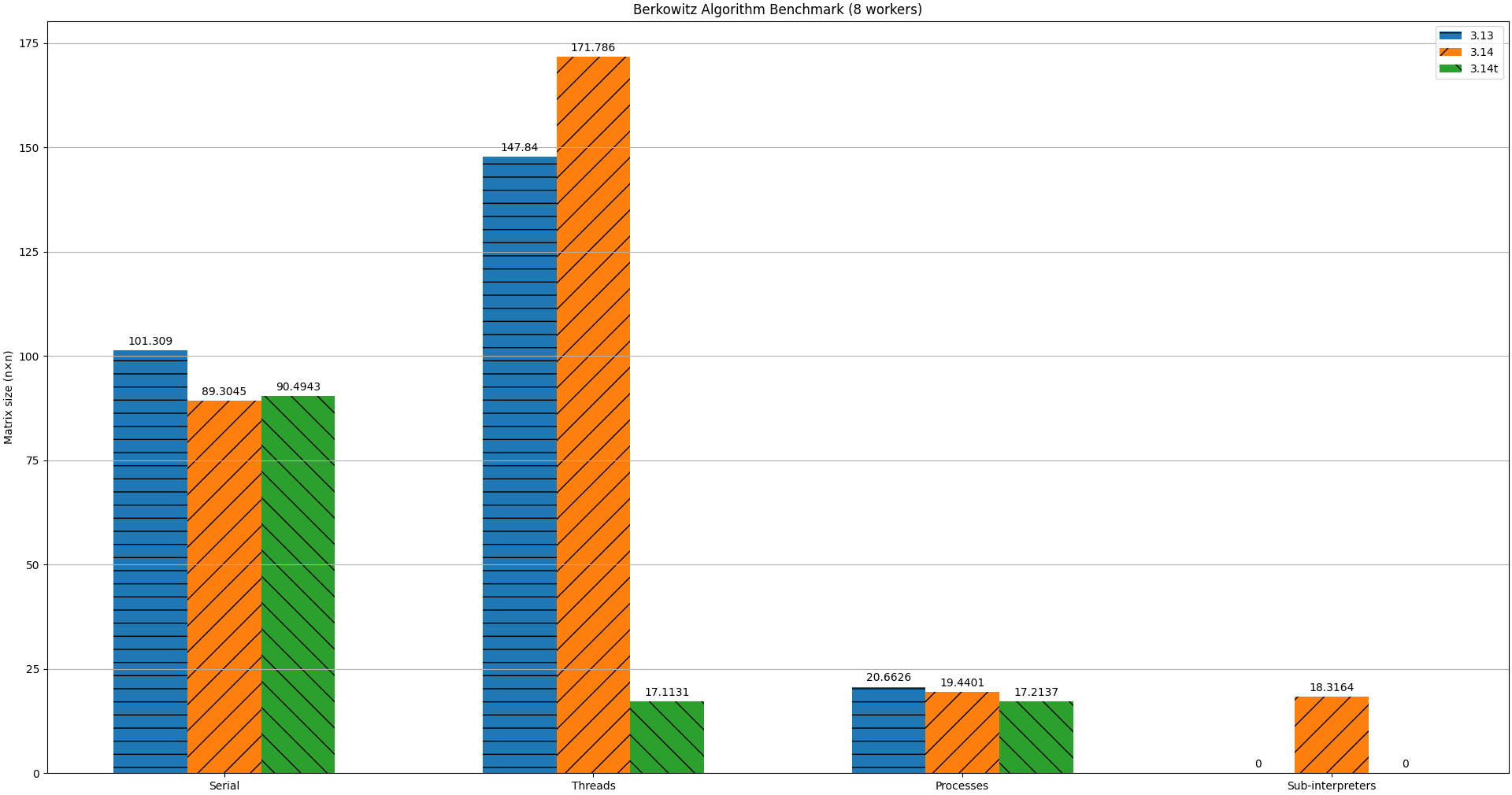
Fig.3. Benchmark Result: Bar Chart
The charts clearly show that Python continues to improve with each release, thanks to the incredible efforts of contributors. As Python users, we are grateful for the ongoing work that keeps making the language faster and more efficient.
For this specific implementation and use case, both Python 3.14 and its free threaded variant (3.14t) outperformed Python 3.13, with Python 3.14 being slightly faster than 3.14t.
As for the parallel implementation, the benefits of parallelization are clearly evident for larger matrices. Among the parallel versions, the free threaded version was the fastest, followed closely by sub-interpreters and multi-processing, with only small differences between them.
Conclusion
Implementing a theoretical algorithm and trying to improve it is both challenging and educational. Working on the Berkowitz algorithm and parallelizing it was an enjoyable experience and while benchmarking proved to be less "pleasant" than the original task, the results provided valuable insights.
One of the most rewarding outcomes was the observed 1.22x average performance improvement between Python 3.13 and 3.14 versions, highlighting the continuous progress in the Python ecosystem. Additionally, the significant performance boost from parallelization, especially with the introduction of free threading, demonstrated that it is a highly effective approach for this type of computational task.
In the end, this project not only validated the theoretical speedups of parallelization but also showcased how improvements in Python's execution model can lead to tangible performance benefits in real-world applications.
